|
Значение качественных задач для изучения физики. Часть 3.
В предыдущей заметке мы рассмотрели две задачи из самого начального раздела школьной физики – «Прямолинейное равномерное движение». Заодно вы смогли проверить свой уровень понимания этих простейших понятий школьной физики в рамках 6-7 классов.
Здесь мы приведем классическую задачу из кинематики на неравномерное движение. Именно подобные задачи вызывают особую трудность у школьников на ЦТ и ЕГЭ, т.к. их решение с помощью стандартных уравнений, используемых для равноускоренного и равнозамедленного движения, невозможно из-за нелинейной зависимости скорости от времени, а незнание интегралов не позволяет аналитически проанализировать ход решения. В подобных ситуациях только графический подход позволяет многократно упростить рассуждения и прийти к правильному результату быстро и надежно с помощью элементарных рассуждений.
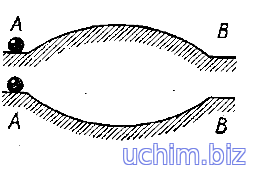
Задача 1. Два шарика начали одновременно и с одинаковой начальной скоростью v0 двигаться по поверхностям, имеющим форму, изображённую на рис. 1. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.
Решение. Рассмотрим систему координат vOt, где v – скорость, t – время, v1(t) и v2(t) – зависимости скоростей шариков от времени, t1 и t2 – моменты времени прохождениям шариками точки В.
Первый очевидный вывод: кривые v1(t) и v2(t) симметричны относительно вертикальных прямых t=t1/2 и t=t2/2 соответственно (это моменты прохождения шариками соответственно самой низкой и самой высокой точек. Отсюда сразу ясно, что v1(t1)=v2(t2)= v0 –равенство скоростей на «выходе», т.е. в точке В.
Первый очевидный вывод: кривая v1(t) целиком лежит ниже горизонтальной прямой v= v0 на промежутке [0;t1], а кривая v2(t) целиком лежит выше горизонтальной прямой v= v0 на промежутке [0;t2]. Вспомним, что графически расстояния, пройденные точками, равны площадям криволинейных трапеций, ограниченных осями координат, кривой v1(t) , прямой t=t1 и кривой v2(t), прямой t=t2 соответственно. Эти площади равны, так как равны расстояния, пройденные шариками. А это возможно, только если точка t1 будет лежать правее точки t2 (рис. 2).
В итоге имеем:
Ответ: Скорости будут одинаковыми. Время движения второго шарика меньше.
С уважением, Жанна Альбертовна
|
| Категория: Советы преподавателей
|
|
|
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
|
